Criptografia Clássica
Dois tipos principais de cifra abrangeram a história da criptografia clássica: as cifras de substituição e as de transposição. Nas cifras de substituição os símbolos do alfabeto do texto plano são substituídos por um ou mais símbolos do alfabeto do texto cifrado de acordo com uma regra, gerando o texto cifrado. Já nas cifras de transposição os símbolos do alfabeto do texto plano são permutados, também de acordo com uma regra, gerando o texto cifrado.
Cifras de Substituição
Atbash
Uma das primeiras cifras de substituição. É vista em passagens da bíblia como em [Jeremias 25:26 - "O rei de Sheshach beberá depois deles" - Sheshach, que significa Babilônia em Atbash (בבל bbl → ששך ššk)].
Trata-se de uma substituição monoalfabética de deslocamento 0 com o alfabeto do texto cifrado na ordem inversa do alfabeto do texto plano. Exemplo com o alfabeto latino:
A |B |C |D |E |F |G |H |I |J |K |L |M |N |O |P |Q |R |S |T |U |V |W |X |Y |Z
Z |Y |X |W |V |U |T |S |R |Q |P |O |N |M |L |K |J |I |H |G |F |E |D |C |B |A
Ganesh -> Tzmvhs
Cifra de substituição simples (monoalfabética)
Trata-se de uma cifra em que cada unidade do texto plano é substituída por uma única unidade do texto cifrado, de acordo com um mapeamento entre os alfabetos do plaintext e do ciphertext, por exemplo:
Alfabeto do plaintext: A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z
Alfabeto do ciphertext: D|G|U|A|S|M|Z|E|R|B|C|I|H|V|Y|P|K|X|Q|N|T|F|W|L|O|J
Ex: GANESH -> ZDVSQE
Cifra de César
Foi uma cifra de substituição monoalfabética utilizada pelo general Julio César em Roma.
Exemplo com o alfabeto latino:
A|B|C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z
C|D|E|F|G|H|I|J|K|L|M|N|O|P|Q|R|S|T|U|V|W|X|Y|Z|A|B
Deslocamento 2
Ganesh -> Icpguj
Quebrando a Cifra de substituição simples
É possível quebrar as cifras de substituição monoalfabética por meio da análise de frequência das letras do ciphertext, desde que se conheça o idioma utilizado. Acontece que nas cifras monoalfabéticas cada letra do plaintext é encriptada sempre para a mesma letra do ciphertext. No exemplo que vimos acima, a letra L será sempre encriptada para a letra I, a letra M será sempre encriptada para a letra H, e assim sucessivamente.
Por exemplo, no idioma inglês a letra E é a mais frequente de todas, aparecendo em 12,70% do total de letras em um texto, seguida dela vem a letra T, que aparece 9,05% das vezes. Sabendo disso, em posse de um ciphertext escrito em inglês, se a letra mais frequente encontrada for a letra K, provavelmente ela corresponde à letra E do plaintext. E se a segunda letra mais frequente for a letra W, provavelmente ela corresponde à letra T do plaintext.
Cifra de Vigenère
Trata-se de uma cifra de substituição polialfabética em que a palavra chave é responsável por especificar o deslocamento de cada letra do plaintext. Desse modo, é impossível realizar diretamente um ataque de frequência como o utilizado nas cifras de substituição monoalfabética, já que uma mesma letra do plaintext pode ser encriptada para diferentes letras no ciphertext, a depender do seu “match” com a palavra chave ao longo do texto.
Quando a palavra chave for menor do que o plaintext, ela deve ser repetida até completar o tamanho do plaintext. A encriptação pode ser descrita algebricamente: se as letras A-Z correspondem aos números 0-25, soma-se o valor numérico da letra no plaintext com o valor numérico de sua letra pareada na chave e aplica-se o resto da divisão por 26, encontrando o valor numérico da letra do ciphertext. Exemplo de encriptação com a chave LEMON:
Plaintext: A|T|T|A|C|K|A|T|D|A|W|N Chave: L|E|M|O|N|L|E|M|O|N|L|E Ciphertext: L|X|F|O|P|V|E|F|R|N|H|R
Note que a primeira letra T foi encriptada para X, enquanto que a segunda letra T foi encriptada para F. Ou seja, a mesma letra do plaintext resultou em letras diferentes no ciphertext. Para decriptar, basta subtrair o valor numérico de cada letra do ciphertext do valor numérico do seu par na chave. Caso resulte em um número negativo, basta somar 26. O resultado dessa operação será o valor numérico da letra no plaintext.
A tabela a seguir é utilizada para facilitar a encriptação e a decriptaçao, dado um plaintext e uma chave.

Quebrando a Cifra de Vigenère (Teste de Kasiski)
Como já vimos anteriormente, a Cifra de Vigenère foi considerada inquebrável por três séculos, até que em 1863 Friedrich Kasiski propôs um ataque que funciona quando o tamanho da chave é menor do que o do plaintext. Para entendermos o Teste de Kasiski, vamos utilizar o mesmo exemplo anterior e considerar que o atacante já saiba o tamanho da chave:
Plaintext: A|T|T|A|C|K|A|T|D|A|W|N Chave: L|E|M|O|N|L|E|M|O|N|L|E Ciphertext: L|X|F|O|P|V|E|F|R|N|H|R
Como o tamanho da chave já é conhecido (5 letras), sabemos que a cada cinco letras do ciphertext o deslocamento realizado para obter tais letras foi exatamente o mesmo. Note que as letras L, V e H, destacadas acima, foram todas obtidas a partir de um mesmo deslocamento. Agora, se temos um conjunto de letras e todas foram obtidas a partir de um mesmo deslocamento, temos diante de nós uma cifra de substituição simples, que é passível de ataque por análise de frequência.
Suponha que o texto do exemplo acima seja muito maior, logo o conjunto que possui as letras L, V e H possui ainda muito mais letras, muitas delas vão se repetindo dentro do conjunto. Como o texto é escrito em inglês, é provável que a letra que mais se repetir dentro desse conjunto foi obtida a partir da encriptação da letra E. Logo, em posse de uma letra do plaintext e de uma letra do ciphertext, é possível descobrir qual a letra da chave que gerou tal deslocamento.
Assim, descobrimos a primeira letra da chave. Para descobrir a próxima letra, basta repetir o processo para formar um novo conjunto (formado pelas letras X, E, R...) e supor que a letra mais abundante desse conjunto foi obtida a partir da encriptação da letra E. Note que isso tudo só é possível quando soubermos o tamanho exato da chave. Na prática, para descobrirmos o tamanho da chave é preciso encontrar padrões de repetições ao longo do ciphertext e a partir do distanciamento dessas repetições obter o tamanho da chave.
Observe a imagem com o ciphertext a seguir e repare na repetição da sequência U-S-E diversas vezes ao longo do texto.

Como o distanciamento dessas repetições é sempre um número múltiplo de 8, um bom palpite para o tamanho da chave seria 8 caracteres. Mas também é possível que o tamanho da chave seja de 4 caracteres. De qualquer forma, com o tamanho da chave em mãos, basta aplicar o Teste de Kasiski para descobrir a chave utilizada e assim quebrar a cifra.
Cifra Autokey
Vimos que a Cifra de Vigenère é quebrável quando o tamanho da chave é menor do que o tamanho do plaintext. A Cifra Autokey foi criada justamente de modo a garantir que o tamanho da chave seja sempre superior ao do plaintext. Para isso, é feito a concatenação entre uma keyword relativamente pequena e o plaintext. O resultado dessa operação é a chave que será utilizada na encriptação.
Por exemplo, se a keyword for QUEENLY e a mensagem for “attack at dawn”, então a chave seria QUEENLYATTACKATDAWN. A partir disso, basta aplicar a Cifra de Vigenère.
Plaintext: A|T|T|A|C|K|A|T|D|A|W|N Chave: Q|U|E|E|N|L|Y|A|T|T|A|C|K|A|T|D|A|W|N Ciphertext: Q|N|X|V|P|V|Y|T|W|T|W|P
Para decriptar a mensagem, o receptor começaria utilizando a keyword previamente definida (QUEENLY), obtendo assim as primeiras 7 letras do plaintext (ATTACKA). Depois, essas 7 letras são concatenadas ao final da keyword e novas letras serão obtidas. O ciclo é repetido até se obter o plaintext final. A Cifra Autokey é mais segura do que as cifras polialfabéticas que usam chaves fixas, já que na Autokey a chave não é repetida dentro de uma mesma mensagem. Portanto, métodos de ataque como o Teste de Kasiski não se aplicam nessa cifra.
Uma grande vulnerabilidade dessa cifra, no entanto, é que o plaintext faz parte da chave. Isso significa que a chave vai certamente conter palavras comuns em diversas posições (ON, AT, IN, THE no inglês ou DE, DO, DA, UMA, SUA, QUE no português). A chave pode ser atacada usando palavras comuns através de tentativas de decriptar a mensagem movendo a palavra pela chave até que textos legíveis apareçam.
Polybus Square
Trata-se de um dispositivo inventado pelos gregos Cleoxenus e Democlitus e aperfeiçoado por Polybius, cujo propósito era dividir os símbolos do texto plano para que pudessem ser representados por um conjunto menor de símbolos. Inicialmente, Polybius sugeriu que os símbolos poderiam ser usados para transmitir mensagens com pares de tochas. Além disso, também foi usada na forma de "knock code" para transmitir mensagens em prisões a partir de barulhos em canos e paredes.
A tabela a seguir é utilizada para encriptar e decriptar mensagens, note que com apenas cinco números é possível representar todas as letras do alfabeto.
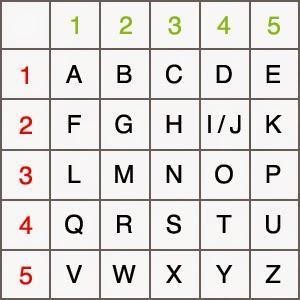
Plaintext: G |A |N |E |S |H Ciphertext: 22|11|33|15|43|23
Cifra Homófona
Trata-se de uma cifra em que os símbolos mais frequentes do plaintext são correspondidos para mais de um símbolo no ciphertext. Foi criada para dificultar a análise estatística baseada em frequência. Observe o mapeamento da imagem a seguir, note que na primeira vez que a letra A aparece, ela é encriptada para 8. Na segunda vez para z, e assim sucessivamente.

Plaintext: Abracadabra Ciphertext: 8FbzHKG7FRi
Cifra Poligráfica
Trata-se de uma cifra em que a substituição se dá mapeando um caractere para um grupo de símbolos, por exemplo:
Alfabeto do plaintext: A|B|C|D... Alfabeto do ciphertext: &A|789|CVD|ZDFG...
Enigma
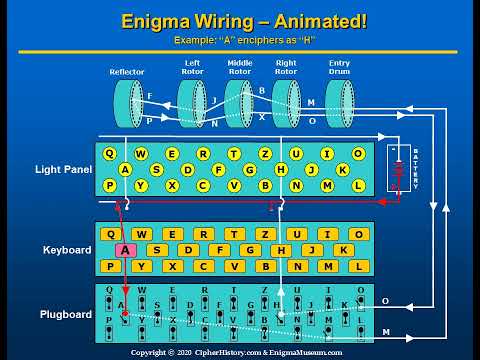
Criada para substituir os métodos "papel e caneta" que eram utilizados até então, a Enigma foi amplamente utilizada pela Alemanha nazista na Segunda Guerra Mundial. Sua quebra teve um grande impacto na história da guerra e na história da computação. Para entender o funcionamento da Enigma, precisamos olhar por dentro para identificar as quatro principais regiões da máquina.

Keyboard: é o input. Composto pelas teclas que serão digitadas quando se quer encriptar ou decriptar uma mensagem.
Lightboard: é o output. Cada vez que uma tecla é pressionada, fecha-se um circuito elétrico e uma das lâmpadas da lightboard se acende. Na encriptação, o keyboard corresponde ao plaintext enquanto que a lightboard fornece o ciphertext. Na decriptação, os papéis se invertem.
Rotor: responsável pela permutação das letras. Em uma face do rotor existem 26 pinos por onde a corrente elétrica pode entrar e na outra face existem 26 pinos por onde a corrente pode sair. No interior de cada rotor, há fios que fazem as trocas de uma letra por outra. A sequência de imagens a seguir mostra como um rotor faz a permutação de uma letra por outra três posições a frente no alfabeto.
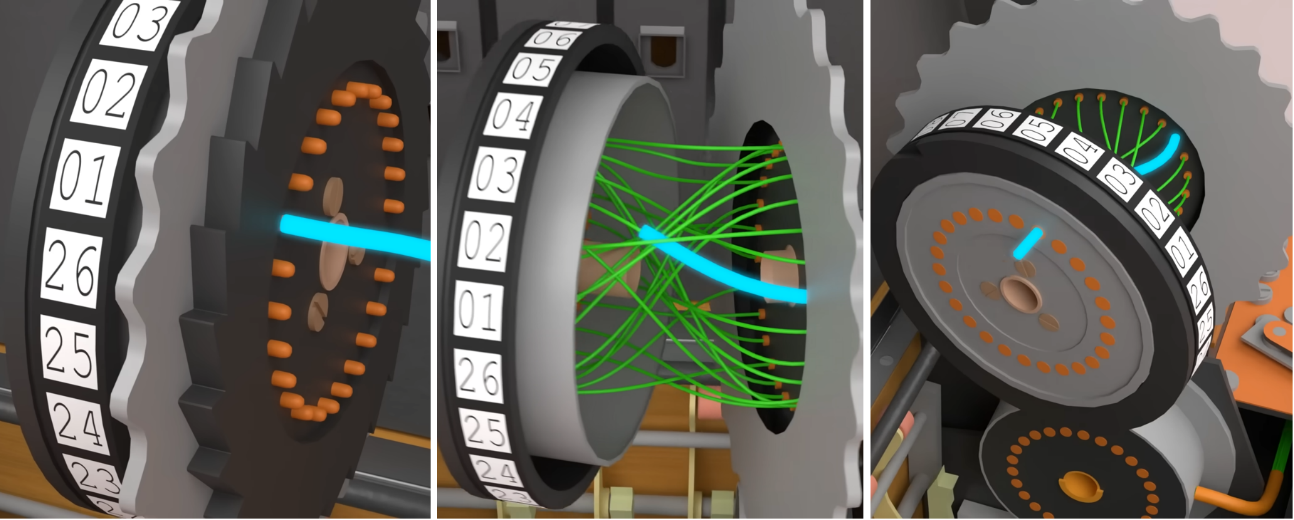
Pressionar uma tecla faz com que o primeiro rotor rotacione uma posição. Como são três rotores em série o simples fato de o rotor girar uma posição faz com que o mapeamento de letras mude completamente. Além disso, o anel de cada rotor possui um entalhe que serve para definir quando ele vai provocar uma rotação no rotor à sua esquerda. Posicionar esse entalhe no número 18, por exemplo, faz com que quando esse número alcança a parte de trás da máquina, o rotor à esquerda rotaciona uma posição, e a partir daí, a cada ciclo de 26 teclas pressionadas o primeiro rotor completará uma volta completa, fazendo com que o segundo rotor rotacione uma posição. Quando o entalhe do segundo rotor alcança a parte de trás da máquina, o terceiro rotor rotaciona uma posição, e a partir daí, a cada volta completa do segundo rotor (26x26 = 676 teclas pressionadas) o terceiro rotor ira rotacionar mais uma posição. A imagem a seguir mostra o entalhe do primeiro rotor posicionado no número 18.

Plugboard: posicionado na frente da máquina, também é responsável pela permutação das letras e aumenta consideravelmente o número de configurações possíveis da máquina. Ao se conectar o plugue da letra A com o da letra U, por exemplo, toda vez que a letra A é pressionada no keyboard, ela é permutada para a letra U antes de passar pela permutação dos rotores. Se um determinado plugue não está conectado com nenhum outro, então a sua letra correspondente não sofre nenhuma permutação no plugboard, sofrendo apenas as permutações dos rotores.
Funcionamento do circuito
O caminho percorrido entre o pressionamento de uma tecla no keyboard e o acendimento de uma lâmpada na lightboard é o seguinte: keyboard -> plugboard -> rotores -> refletor -> rotores -> plugboard -> lightboard. O vídeo a seguir mostra a letra A sendo encriptada para a letra H. Repare que os plugues A e M estão conectados na plugboard, assim como os plugues H e O.
Ao se pressionar a tecla A, ela é permutada para M na plugboard, que segue em direção aos rotores. O primeiro rotor permuta M para B, o segundo rotor permuta B para J e o terceiro rotor permuta J para F. Então o refletor permuta F para P. Na volta, o terceiro rotor permuta P para N, o segundo rotor permuta N para X e o primeiro rotor permuta X para O. Finalmente, a plugboard permuta O para H e a lightboard acende a lâmpada da letra H.
Note que se a tecla H tivesse sido pressionada nessas mesmas configurações, a lâmpada da letra A teria sido acesa.
Quantas configurações da Enigma são possíveis?
Para responder essa pergunta, vamos considerar o modelo de configuração mais usado durante a Segunda Guerra Mundial: os operadores dispunham de 5 rotores, sendo que 3 eram selecionados para serem utilizados em cada dia. Utilizava-se sempre 10 cabos na plugboard, o que significa que 20 letras sofriam permutação na plugboard, enquanto 6 não sofriam.
Dos 5 rotores, selecionar 3 significa: 5 x 4 x 3 = 60
Posição inicial dos rotores: 26 x 26 x 26 = 17.576
Posição do entalhe em cada rotor 26 x 26 = 676 (a posição do entalhe do terceiro rotor é irrelevante já que ele não provoca giro em nenhum rotor)
Formas diferentes de se conectar os 10 cabos da plugboard: 150.738.274.937.250
O produto das combinações acima resulta em 107.458.687.327.250.619.360.000 ou 1,07 x 10²³. Para se testar 1,07 x 10²³ configurações, se reuníssemos 100.000 voluntários e cada um testasse uma configuração por segundo, ainda levaríamos o dobro da idade do universo para se testar todas as possibilidades.
Protocolo de encriptação
Mensalmente, os operadores das máquinas Enigma recebiam os “codebooks”, que eram instruções para a configuração da máquina para cada dia do mês. A imagem a seguir mostra um codebook obtido pelos Aliados.
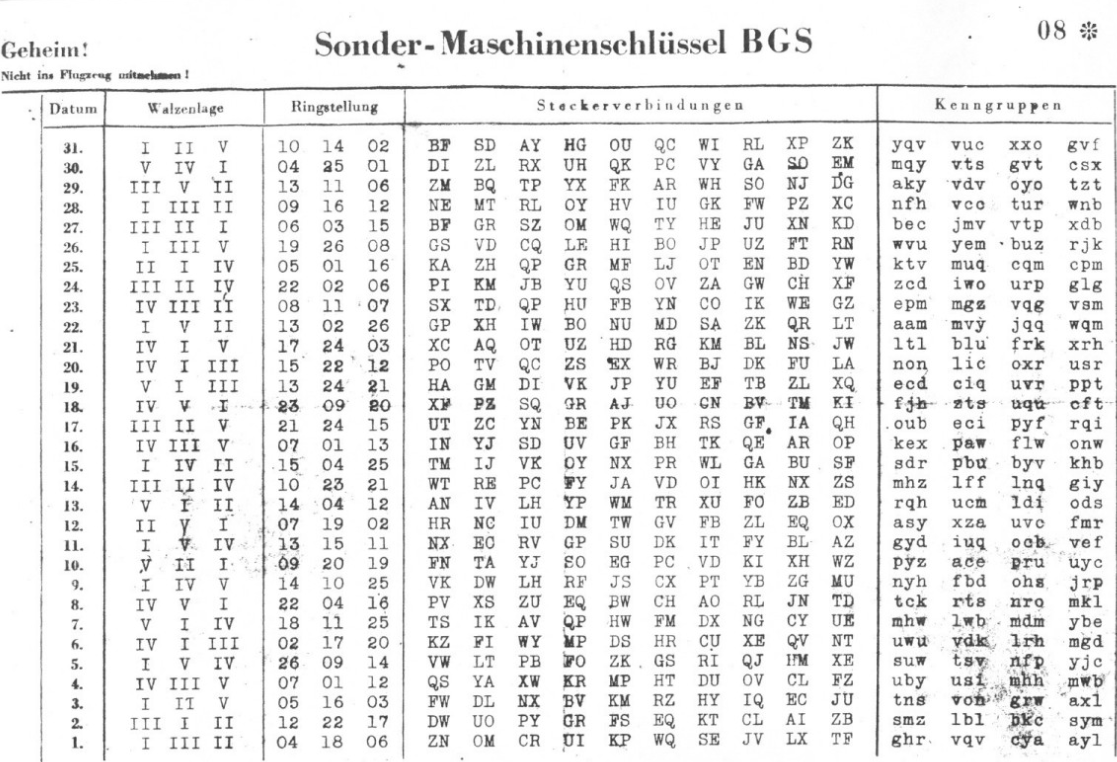
No dia 31, por exemplo, as configurações seriam as seguintes:
A segunda coluna mostra que os rotores I, II e V seriam usados naquele dia
A terceira coluna mostra que o entalhe em cada rotor seria nas posições 10, 14 e 02 respectivamente
A quarta coluna mostra os pares de conexões na plugboard
A quinta coluna mostra os grupos indicadores, que são enviados junto ao ciphertext para identificar em qual dia a mensagem foi enviada.
Acontece que se uma grande quantidade de mensagens fossem encriptadas utilizando a mesma configuração a Enigma ainda seria passível de ataques por frequência. Por exemplo, imagine que os Aliados interceptassem muitas mensagens encriptadas com a mesma configuração inicial. Uma análise de frequência na primeira letra de cada ciphertext obtido permitiria concluir que a letra mais frequente foi encriptada a partir da letra E (no idioma alemão a letra E é a mais comum, assim como no inglês). Portanto, a cada mensagem a ser encriptada os operadores da Enigma eram instruídos a seguir os seguintes passos:
Posicionar os rotores na ordem, conforme codebook;
Posicionar o entalhe de cada rotor conforme codebook;
Conectar os cabos da plugboard conforme codebook;
Escolher um grupo indicador para enviar junto ao ciphertext;
Escolher a posição inicial dos rotores (ex: HTX);
Escolher uma chave de três letras (ex: RZU);
Digitar a chave escolhida duas vezes. Ex: Plaintext: RZURZU Ciphertext: JIOWQP
Resetar a posição inicial dos rotores para a chave escolhida (RZU);
Encriptar a mensagem com as novas configurações.
Esse protocolo eliminava qualquer chance de análise por frequência, já que agora cada mensagem enviada tinha sua própria configuração, definida pelo operador. Para decriptar, o receptor da mensagem não sabia a chave RZU escolhida pelo emissor, mas a posição inicial dos rotores (HTX) era transmitida na mensagem. Então bastava ele repetir os primeiros três passos da encriptação, posicionar os rotores (HTX) e digitar JIOWQP em sua Enigma que a lightboard acenderia RZURZU. Assim, o receptor ajustaria a posição dos rotores para RZU e seria capaz de decriptar a mensagem.
Você deve estar se perguntando o porquê de digitar a chave escolhida duas vezes, visto que o protocolo funcionaria da mesma forma se a chave escolhida fosse digitada apenas uma vez. Imagine que durante a transmissão do ciphertext JIOWQP o tempo estava ruim e houve interferências de modo que o receptor recebeu JIOWQT. Ao digitar esse ciphertext na Enigma ele obteve RZURZH e pode concluir que a chave escolhida pelo emissor foi RZU ou RZH.
Se a chave escolhida fosse digitada apenas uma vez, sempre que houvesse interferência na transmissão o receptor iria obter uma chave inútil, sendo incapaz de decriptar a mensagem e precisaria que o emissor enviasse a mensagem novamente, causando atrasos na comunicação. Contudo, a repetição de chave era uma vulnerabilidade que os poloneses exploraram, sendo capazes inclusive de quebrar a Enigma antes do início da guerra, quando os alemães ainda utilizavam um conjunto de apenas 3 rotores e somente 6 cabos na plugboard.
Liderados pelo matemático Marian Rejewski e com a ajuda de espiões franceses, os polonoses foram capazes de deduzir os fios internos dos rotores por meio da aplicação de álgebra abstrata e ainda construíram a primeira máquina elétrico-mecânica capaz de sistematicamente quebrar a Enigma, batizada de “Bombe”.
Com o início da guerra, os alemães aumentaram consideravelmente o número de configurações possíveis da Enigma, além de abortarem o protocolo de digitar a chave escolhida duas vezes, fazendo com que a bombe polonesa se tornasse ineficiente. Porém, o trabalho secreto dos poloneses mostrou aos aliados ingleses que a Enigma era quebrável. Sem esse pontapé inicial, o trabalho de Alan Turing e dos criptógrafos do Bletchley Park seria muito mais difícil.
Vulnerabilidades da Enigma
A cada mensagem enviada, o operador escolhia 6 letras para encriptá-la, sendo as três primeiras para a posição inicial dos rotores e as três últimas seriam a chave que seria de fato utilizada. Os operadores eram orientados a escolher 6 letras aleatórias, mas muitos deles eram negligentes e facilitavam o trabalho dos aliados ao escolherem sequencias de letras como LON-DON, BER-LIN ou até mesmo teclas vizinhas do keyboard como ASD-FGH. Um caso muito famoso foi o de um soldado alemão que frequentemente utilizava o nome da namorada dele CIL-LIE, então esse método de codebreaking foi batizado de “Cillies”.
Outra vulnerabilidade muito explorada eram os relatórios diários cujo formato do texto raramente mudava. Muitos submarinos, por exemplo, enviavam relatórios de previsão do tempo tão padronizados de modo que os analistas podiam dar palpites certeiros de qual posição estaria o plaintext “clima”. Em regiões menos movimentadas, era comum unidades militares enviarem mensagens como “nada incomum” ou “nada a reportar” – outra frequente repetição que os britânicos usaram a seu favor.
Cifras de Transposição
Transposição Colunar
Para encriptar por meio da cifra de transposição por coluna, deve-se escrever a chave na primeira linha de uma tabela. Em seguida, escreve-se o texto da esquerba para a direita e de cima pra baixo, e lê-se o texto na vertical, seguindo a ordem alfabética das letras da chave. Exemplo de encriptação com a chave CRIVO:
Plaintext: Somos o Ganesh Chave: CRIVO
Ciphertext: S nm ssa ooeoGH
Para decriptar, escrevemos o texto cifrado na tabela na direção vertical seguindo a ordem alfabética das letras da chave, em seguida lemos o texto na horizontal na direção usual.
Rail Fence
Na cifra Rain Fence, o plaintext é escrito para baixo diagonalmente em "trilhos" sucessivos de uma cerca imaginária, movendo-se para cima quando o trilho inferior é alcançado, e para baixo novamente quando o trilho superior é alcançado e assim por diante até que todo o plaintext seja escrito. O ciphertext é então obtido lendo-se por linhas. A imagem a seguir mostra um exemplo para três trilhos.
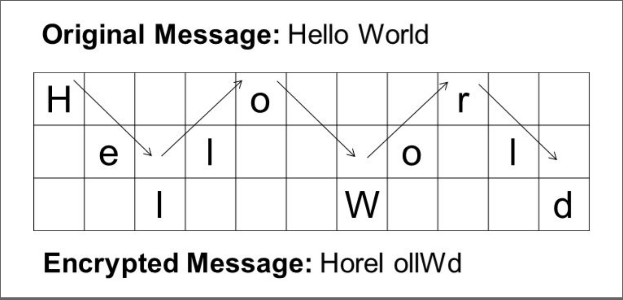
Para decriptar, basta construir uma matriz em que o número de colunas é igual ao tamanho do ciphertext e o número de linhas é igual à chave (número de trilhos). Depois basta percorrer a matriz em zigzag, marcando com asterisco as células que receberão letras:
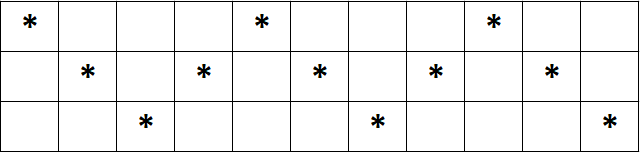
Por fim, basta preencher a matriz horizontalmente com as letras do ciphertext e lê-la de acordo com o zigzag.
Esteganografia
A esteganografia (do grego ‘escrita escondida’) é o uso de de técnicas para ocultar a existência de uma mensagem dentro da outra, uma forma de segurança por obscurantismo. A diferença entre esteganografia e criptografia é que a primeira preocupa-se em ocultar a existência da mensagem, e a segunda o seu significado.
Método NULL
A simples representação também remete à esteganografia, que é uma técnica para omitir uma mensagem dentro de outra, com o objetivo de fazer com que uma forma escrita seja camuflada em outra a fim de mascarar sua própria existência. Uma técnica simples de esteganografia é o método NULL, no qual a letra do meio de cada palavra da mensagem original compõe a mensagem que se deseja esconder.
Last updated