Criptografia Moderna
Até o momento, todas as cifras que descrevemos eram utilizadas com o objetivo de se garantir a confidencialidade, e os plaintexts eram compostos basicamente por sequencias de letras. Contudo, com a entrada da computação no cenário e a chegada da era moderna, a criptografia expandiu seus campos de atuação, de modo que hoje lidamos com sequencias de bits, que podem significar letras, pixels de uma imagem, áudios, entre outros.
Por exemplo, a sequência de bits 01000001 em um arquivo de extensão (.txt) significa a letra A, conforme tabela ASCII. Já a sequencia 00000000 em um arquivo (.jpg) significa um pixel preto e a sequencia 11111111 significa um pixel branco.
Simétrica
No sistema de criptografia simétrica apenas uma chave é utilizada, tanto para encriptar quanto para decriptar a mensagem.
One Time Pad
Para estudar a cifra One Time Pad (OTP), é preciso primeiro compreender as propriedades do operador lógico XOR (ou exclusivo). Trata-se de uma operação sobre dois ou mais valores lógicos que produz um valor verdadeiro apenas se a quantidade de operadores verdadeiros for ímpar. A Tabela-verdade para o XOR de duas entradas é a seguinte:
Abaixo são apresentadas algumas propriedades do operador lógico XOR:
Comutativa: A ⊕ B = B ⊕ A
Associativa: A ⊕ (B ⊕ C) = (A ⊕ B) ⊕ C
Identidade: A ⊕ 0 = A
Auto-inversiva: A ⊕ A = 0
A ⊕ B = C ↔ C ⊕ B = A ↔ C ⊕ A = B
O funcionamento da cifra One Time Pad é o seguinte: o ciphertext é o resultado do XOR bit a bit entre o plaintext e a chave. Para decriptar, o plaintext é simplesmente o resultado do XOR bit a bit entre o ciphertext e a chave. As funções que definem a encriptação e a decriptação são:
E(m, k) = m ⊕ k = c D(c, k) = c ⊕ k = m
Plaintext: 0|1|1|0|1|0|0|0|1|1|0|1 Chave: 1|0|1|1|0|0|1|1|1|0|0|1 Ciphertext: 1|1|0|1|1|0|1|1|0|1|0|0
A cifra OTP é muito boa do ponto de vista de performance computacional, tudo que o processador precisa fazer é o XOR da mensagem com a chave, o que é extremamente simples e rápido para os computadores atuais. Entretanto, é muito difícil vê-la sendo aplicada na prática. O motivo disso é que as chaves são essencialmente tão longas quanto as mensagens.
Suponha que Alice e Bob queiram se comunicar usando a OTP. Alice quer enviar uma mensagem encriptada para Bob, mas primeiro ela precisar enviar por um canal seguro uma chave que seja tão longa quanto a mensagem. Ora, se ela possui um meio seguro de transmitir uma chave longa, ela pode simplesmente usar esse meio para transmitir diretamente o plaintext, sem que nenhuma criptografia seja necessária.
Então, o fato de a chave ser tão longa quanto a mensagem faz com que a One Time Pad seja bem difícil de ser aplicada na prática. Contudo, a ideia por trás da cifra é muito útil, e veremos isso mais adiante. Por ora, vamos analisar duas vulnerabilidades que podem ser exploradas na cifra.
Many Time Pad
O Many Time Pad ocorre quando duas mensagens diferentes são encriptadas utilizando-se a mesma chave. Isso permite que um atacante intercepte os dois ciphertexts e, utilizando a propriedade auto-inversiva do XOR, obtenha como resultado o XOR entre os dois plaintexts.
c1 = m1 ⊕ k c2 = m2 ⊕ k c1 ⊕ c2 = m1 ⊕ k ⊕ m2 ⊕ k = m1 ⊕ m2 ⊕ k ⊕ k = m1 ⊕ m2
A imagem a seguir exemplifica como o conteúdo de dois plaintexts foram descobertos por terem sido encriptados a partir de uma mesma chave.
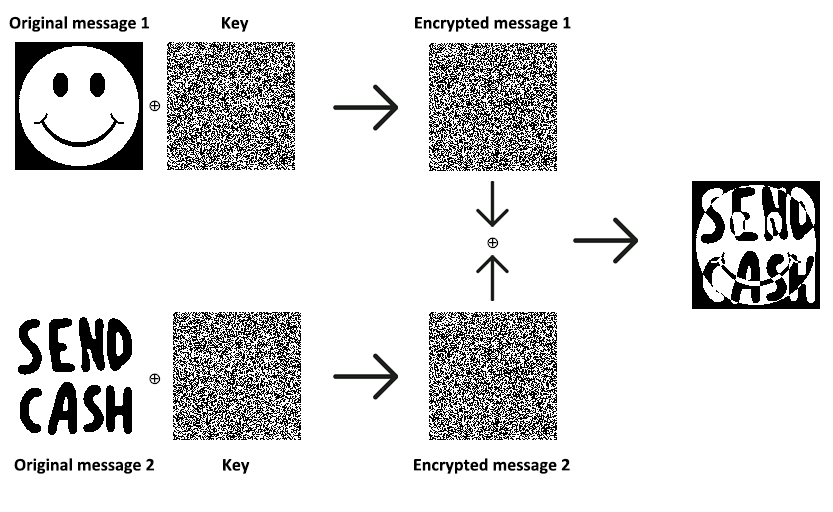
Outra forma de se explorar o Many Time Pad é através do método Crib Dragging. Ele ocorre quando o atacante já conhece parcialmente o conteúdo de um dos plaintexts, e, em posse de m1 ⊕ m2, é capaz de obter parte do conteúdo do segundo plaintext. A partir disso, ele consegue deduzir mais algum trecho de m2 e obter novos trechos de m1. Esse ciclo se repete até que ambos os plaintexts tenham sido recuperados.
Considere o exemplo a seguir: o atacante interceptou dois ciphertexts de 29 caracteres cada, sendo que ambos foram encriptados com a mesma chave. Assim, o atacante obteve m1 ⊕ m2 e considere ainda que o atacante sabe que o começo de m1 é “BOMDIA”.
Fazendo o XOR entre os primeiros 6 caracteres de m1 e (m1 ⊕ m2), o atacante recupera os 6 primeiros caracteres de m2:
Em posse dos primeiros 6 caracteres de m2, o atacante pode deduzir que os próximos 4 caracteres são “UDAR”, completando a frase “VOUESTUDAR”.
Fazendo o XOR entre os caracteres 7-10 de m2 e (m1 ⊕ m2), o atacante recupera os caracteres 7-10 de m1:
Em posse dos primeiros 10 caracteres de m1, o atacante pode deduzir que o próximo caractere é “O”, completando a frase “BOMDIAAMIGO”.
Fazendo o XOR entre o caractere 11 de m1 e (m1 ⊕ m2), o atacante recupera o caractere 11 de m2:
Em posse dos primeiros 11 caracteres de m2, o atacante pode então deduzir que os próximos caracteres são “ATEMATICA”, completando a frase “VOUESTUDARMATEMATICA”.
Fazendo o XOR entre os caracteres 12-20 de m2 e (m1 ⊕ m2), o atacante recupera os caracteres 12-20 de m1:
Em posse dos primeiros 20 caracteres de m1, o atacante pode então deduzir que os próximos caracteres são “UITO”, completando a frase “BOMDIAAMIGOBOBVOCEEMUITO”.
Fazendo o XOR entre os caracteres 21-24 de m1 e (m1 ⊕ m2), o atacante recupera os caracteres 21-24 de m2:
Em posse dos primeiros 24 caracteres de m2, o atacante pode então deduzir que os últimos caracteres são “TORIA”, completando a frase “VOUESTUDARMATEMATICAEHISTORIA”.
Finalmente, fazendo o XOR entre os caracteres 25-29 de m2 e (m1 ⊕ m2), o atacante recupera os caracteres 25-29 de m1:
Assim, o atacante conseguiu recuperar m1: “Bom dia amigo Bob você é muito lindo” e m2: “Vou estudar matemática e história”.
Bit Flipping
O bit-flipping é um ataque à integridade da cifra que permite ao atacante alterar o ciphertext de modo que, após a mensagem ser decriptada, o receptor receberá um conteúdo diferente do plaintext original, mesmo que o atacante não saiba qual chave foi utilizada. Esse ataque é possível quando o atacante conhece o conteúdo original da mensagem ou apenas parte dele.
Suponha que um atacante saiba que o conteúdo inicial de uma mensagem seja “Envie R$1000,00 para Ana”. Então, o ciphertext deste trecho da mensagem seria:
c = “Envie R$1000,00 para Ana” ⊕ key
Antes que o ciphertext chegue ao receptor da mensagem, o atacante pode intercepta-la e fazer a seguinte operação:
c’ = c ⊕ (“Envie R$1000,00 para Ana” ⊕ “Envie R$1000,00 para Eve”)
Temos que c = “Envie R$1000,00 para Ana” ⊕ key, então
c’ = “Envie R$1000,00 para Ana” ⊕ key ⊕ “Envie R$1000,00 para Ana” ⊕ “Envie R$1000,00 para Eve”
c’ = “Envie R$1000,00 para Eve” ⊕ key
Ao receber c’, o receptor da mensagem vai decriptá-la fazendo o XOR com a chave key e vai obter uma mensagem diferente do plaintext original, sem perceber que seu conteúdo foi adulterado. Para prevenir este tipo de ataque, são utilizados mecanismos que asseguram a integridade da mensagem, como o MAC (Message Authentication Code) e assinaturas digitais, de modo que ao decriptar a mensagem, o receptor seja capaz de perceber que seu conteúdo foi alvo de ataque.
Cifra de Fluxo (Stream Cipher)
Vimos anteriormente que a cifra OTP é raramente aplicada na prática devido ao fato de a chave ser do mesmo tamanho da mensagem. A cifra de fluxo (stream cipher) foi criada justamente para superar esse problema. A cifra de fluxo conta com uma função PRG (Pseudo-Random Generator) que gera bits pseudo-aleatórios a partir de uma semente. Assim, a chave key inicial, embora seja menor do que a mensagem, pode ser expandida para uma chave maior, chamada de keystream, que tem pelo menos o mesmo tamanho da mensagem.
Com a keystream e o plaintext em mãos, a cifra de fluxo funciona da mesma forma que a One Time Pad, sendo passível também dos mesmos ataques.
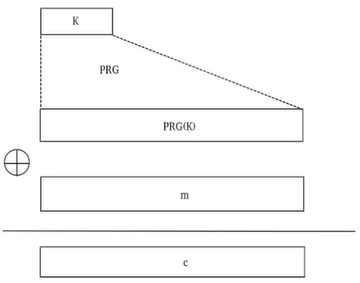
É importante que a função PRG seja imprevisível. Isso significa que dado n bits gerados a partir de uma PRG, um atacante seria incapaz de prever qual seria o (n+1)º bit, independentemente do valor de n.
Imagine uma situação em que o atacante já saiba de antemão os primeiros 24 bits de um plaintext. Fazendo o XOR com o ciphertext interceptado ele pode descobrir os primeiros 24 bits da keystream. Se a PRG fosse previsível, em posse desses 24 bits da keystream, ele poderia descobrir o 25º, e em posse desses 25, o 26º, e assim sucessivamente até descobrir a keystream inteira. Mas sendo a PRG imprevisível, ele é incapaz de descobrir toda a keystream, mesmo tendo obtido os bits iniciais.
Cifra de Bloco (Block Cipher)
A block cipher é uma cifra que opera sobre grupos de tamanho fixo de bits, chamados de blocos. Cada bloco é encriptado através de repetidas iterações, a depender do algoritmo utilizado.
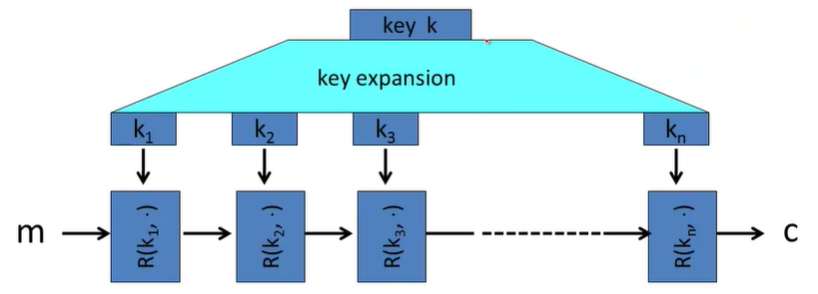
Na encriptação de cada bloco m, a chave k é expandida em uma sequência de chaves k1...kn e o bloco passa por diversas Round Functions até ser obtido o ciphertext c. As round functions garantem o “efeito avalanche” da cifra, de modo que se apenas 1 bit de m for alterado, um bloco c totalmente diferente será obtido.
No algoritmo DES (Data Encryption Standard), o tamanho de cada bloco m é de 64 bits, o tamanho da chave k é de 56 bits e são aplicadas um total de 16 round functions até que o ciphertext c seja obtido. As round functions nesse algoritmo funcionam através da Feistel Network. Com o avanço da capacidade de processamento dos computadores, uma chave de 56 bits passou a ser suscetível a ataques de força bruta, de modo que o DES foi substituído pelo 3DES (Triple Data Encryption Standard), que conta com uma chave de 168 bits e 48 round functions.
No algoritmo AES (Advanced Encryption Standard), o tamanho de cada bloco m é de 128 bits, o tamanho da chave k pode ser 128, 192 ou 256 bits e são aplicadas um total de 10 round functions até que o ciphertext c seja obtido. As round functions nesse algoritmo funcionam através da Substitution-Permutation Network.
Para decriptar cada bloco, o algoritmo utilizado é o inverso daquele usado na encriptação, ou seja, as round functions são aplicadas na ordem inversa.
Modos de Operação
Os algoritmos utilizados nas cifras de bloco são determinísticos. Isso significa que um mesmo plaintext m, ao ser encriptado com a mesma chave k, sempre resultará no mesmo ciphertext c. Numa situação em que uma mensagem possui muitos blocos idênticos, muitos blocos do ciphertext serão iguais, possibilitando a um atacante uma análise por frequência.
Diante disso, diversos modos de operação foram propostos para garantir, dentre outras coisas, que dois blocos idênticos no plaintext resultem em blocos diferentes no ciphertext.
Electronic codebook (ECB)
O mais simples dos modos de operação (e que não deve ser mais usado) é o ECB. Nele, a mensagem é dividida em blocos e cada bloco é encriptado separadamente um do outro. A encriptação é paralelizada, ou seja, para se encriptar o bloco x não é preciso esperar pela encriptação do bloco (x-1). Na prática, isso significa que um processador de dois núcleos, por exemplo, pode usar um núcleo para encriptar os blocos pares e outro para encriptar os blocos ímpares, acelerando o processo.
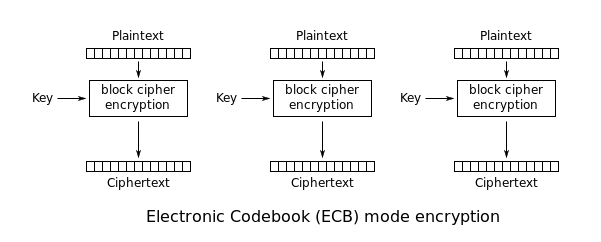
A grande fraqueza desse modo de operação é o fato de blocos de plaintext iguais serem encriptados para blocos de ciphertext iguais. Observe a primeira imagem a seguir, note que os pixels brancos ao redor do pinguim são todos idênticos, assim como os pixels pretos das penas e os pixels laranjas das patas.
Na segunda imagem vemos que todos os pixels brancos foram encriptados exatamente para o mesmo pixel, assim como todos os pixels pretos foram encriptados para o mesmo pixel. Embora a cor de cada pixel individual seja encriptada, a imagem geral ainda pode ser discernida, pois o padrão de pixels de cores idênticas no original permanece na versão criptografada.
Cipher block chaining (CBC)
O próximo modo de operação é o CBC. Nele, a mensagem é dividida em blocos e, antes de passar pelo algoritmo de encriptação, cada bloco de plaintext é XOReado com o bloco de ciphertext anterior. Como o primeiro bloco não possui bloco anterior, é utilizado um vetor de inicialização (IV), que possui uma sequência de bits aleatórios. A encriptação é sequencial, ou seja, para se encriptar o bloco x é preciso esperar pela encriptação do bloco (x-1). Na prática, isso significa que um processador de oito núcleos, por exemplo, vai acabar levando o mesmo tempo para encriptar que um processador de apenas um núcleo.
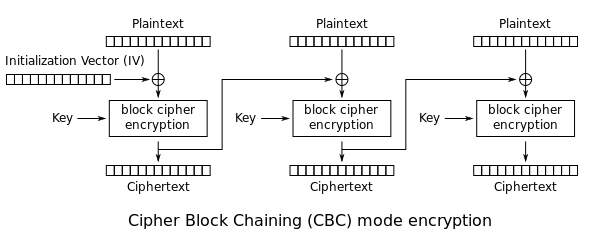
Por outro lado, a decriptação é paralelizada, ou seja, para se decriptar o bloco x não é preciso esperar pela decriptação do bloco (x-1).
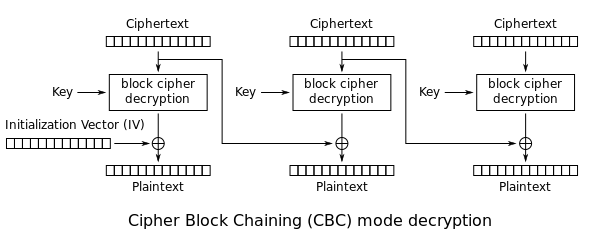
Existem ainda diversos outros modos de operação, como PCBC, CFB, OFB e CTR.
Ataques às cifras de bloco
No modo de operação CBC, se o atacante conhecer o Initialization Vector ou parte dele, é possível fazer um ataque bit-flipping na decriptação que altera o conteúdo do plaintext no primeiro bloco, conforme ilustra a imagem a seguir.
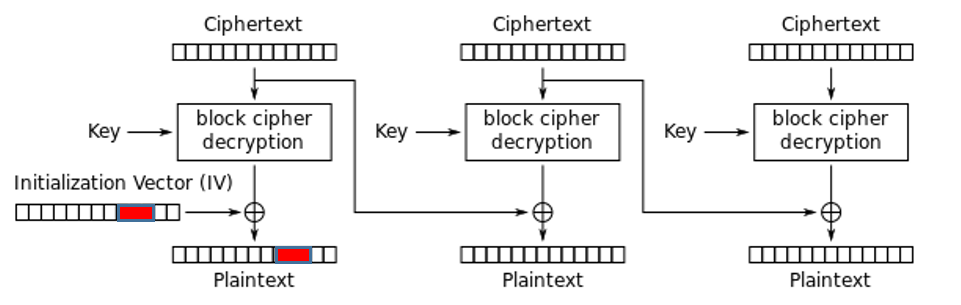
Para prevenir este tipo de ataque, podem ser utilizados mecanismos MAC e assinaturas digitais, assim como nas cifras de fluxo, ou o usuário pode simplesmente preencher o primeiro bloco com bits de “lixo”, que são irrelevantes para o conteúdo da mensagem. Outro ataque associado ao modo de operação CBC é o Padding Oracle Attack, que pode ocorrer quando o tamanho da mensagem não é múltiplo do tamanho do bloco.
Por exemplo, imagine que uma mensagem de 1320 bits seja encriptada utilizando o algoritmo AES. Nesse algoritmo, o tamanho de cada bloco é 128 bits. Logo, são encriptados 10 blocos (10 * 128 = 1280 bits) e ainda restam 40 bits. Para completar o 11º bloco a ser encriptado, é necessário um preenchimento (padding) de 88 bits, que se for feito de maneira incorreta, pode permitir que um atacante descubra o conteúdo de toda a mensagem.
Assimétrica
No sistema de criptografia assimétrica são usadas duas chaves distintas, uma para encriptação e outra para decriptação. A chave de encriptação é pública e é diferente da chave de decriptação, que é privada.
RSA
O mais conhecido dos sistemas de criptografia assimétrica é o método RSA. Este método foi publicado em 1977 por R.L. Rivest, A. Shamir e L. Adleman. As letras RSA correspondem às iniciais dos inventores do método. Para implementar o método RSA, um usuário deve criar uma chave pública “n” que é o produto de dois números primos grandes “p” e “q”, que devem ser escolhidos aleatoriamente e mantidos secretos. Além do número n, o usuário deve escolher um inteiro “e”, que será usado na encriptação, e calcular o seu inverso multiplicativo “d”, que será utilizado na decriptação.
Assim, o par (n, e) é a chave pública utilizada na encriptação, enquanto que a tripla (p, q, d) é a chave privada utilizada na decriptação. A geração das chaves ocorre da seguinte maneira:
Escolha de forma aleatória dois números primos grandes p e q, da ordem de 10^100 no mínimo.
Calcule n = pq
Calcule a função totiente de Euler: Φ(n) = (p-1)(q-1)
Escolher um inteiro e tal que 1 < e < Φ(n), de forma que e e Φ(n) sejam primos entre si, ou seja, mdc(e, Φ(n)) = 1
Calcule d de forma que de ≡ 1 (mod Φ(n)), ou seja, o resto da divisão de de por Φ(n) é 1
Para encriptar um plaintext m em um ciphertext c, basta fazer uma potenciação modular:
m^e ≡ c mod n
Ou seja, o ciphertext c é o resto da divisão de m^e por n. Note que para encriptar foi utilizada somente a chave pública: o par (n, e).
Para decriptar o ciphertext c e recuperar o plaintext m, basta fazer outra potenciação modular:
c^d ≡ m mod n
Ou seja, o plaintext m é o resto da divisão de c^d por n.
Quebrar o método RSA é teoricamente simples, basta fatorar o número n e encontrar os seus fatores primos p e q. O obstáculo é de natureza tecnológica: por se tratar de números muito grandes, encontrar p e q com a tecnologia que temos atualmente levaria dezenas de milhares de anos.
Exemplo de aplicação do RSA
Suponha que Bob e Alice desejam se comunicar utilizando a criptografia RSA. Para receber mensagens encriptadas de Alice, Bob deve fornecer uma chave pública (n, e) que será utilizada por Alice e guardar em segredo a chave privada (p, q, d). Para efeitos didáticos, vamos considerar números pequenos.
Bob escolhe os primos p = 11 e q = 13.
n = p.q = 11.13, n = 143
Φ(n) = (p-1)(q-1) = 10.12, Φ(n) = 120
Bob escolhe e = 7, 7 e 120 são primos entre si.
Bob calcula d.e ≡ 1 mod 120 e obtém d = 103. De fato, d.e = 7*103 = 721. O resto da divisão de 721 por 120 é 1.
Suponha que o plaintext seja por exemplo apenas a letra “f”, cujo valor decimal na Tabela ASCII é 102. Para encriptar, Alice deve utilizar a chave pública (n, e):
m^e ≡ c mod n 102^7 ≡ c mod 143
O resto da divisão de 102^7 por 143 é 119. Portanto o ciphertext é c = 119. Para decriptar, Bob deve utilizar outra potenciação modular:
c^d ≡ m mod n 119^103 ≡ m mod 143
Com auxílio de um sistema computacional algébrico, Bob verifica que o resto da divisão de 119^103 por 143 é m = 102. Assim, Bob recupera o plaintext original.
Last updated